La estadística es la rama de las matemáticas que se ocupa de analizar e interpretar grandes cantidades de datos. Sus fundamentos fueron establecidos a finales del siglo XIX, principalmente por los polímatas británicos Francis Galton y Karl Pearson.
- Figura clave: Francis Galton (1822–1911)
- Campo: Teoría de números
- Antes:
- 1774 Laplace muestra el patrón de distribución esperado alrededor de la norma.
1809 Gauss desarrolla el método de mínimos cuadrados para encontrar la mejor función continua para un conjunto de datos. - 1835 Adolphe Quetelet defiende el uso de la curva de Gauss para modelos de datos sociales.
- Después: 1900 Karl Pearson propone la prueba F2 para determinar las diferencias entre frecuencia esperada y observada.
Orígenes de la estadística
La estadística estudia los patrones de los datos registrados para decidir si son significativos o aleatorios. Sus orígenes se remontan a los esfuerzos de matemáticos del siglo XVIII, como Pierre-Simon Laplace, por identificar los errores de observación en la astronomía. En cualquier conjunto de datos científicos, lo más probable es que los errores sean muy pequeños, y solo es probable que unos pocos sean grandes. Al plantear observaciones en un gráfico, crean una curva en forma de campana, con un pico en el resultado más probable, o «norma», en el centro. En 1835, el matemático belga Adolphe Quetelet constató que características de una población humana como la masa corporal describen una curva de este tipo –en la que los valores próximos a la media son los más frecuentes, y los valores superiores e inferiores, menos frecuentes–, y creó el índice Quetelet para indicar la masa corporal (hoy llamado IMC).
Lo habitual al plantear en un gráfico dos variables, tales como la altura y la edad, es obtener una serie de puntos desordenados que no se pueden unir en una línea definida. En 1809, el matemático alemán Carl Friedrich Gauss dio con una ecuación para obtener la línea de «mejor ajuste» para mostrar la relación entre las variables. Gauss empleó el método llamado de «mínimos cuadrados», consistente en sumar los cuadrados, que es utilizado todavía hoy por los estadísticos. En la década de 1840, matemáticos como Auguste Bravais buscaron un nivel de error aceptable para dicha línea, y trataron de establecer la utilidad del punto medio o la mediana de un conjunto de datos.
Correlación y regresión
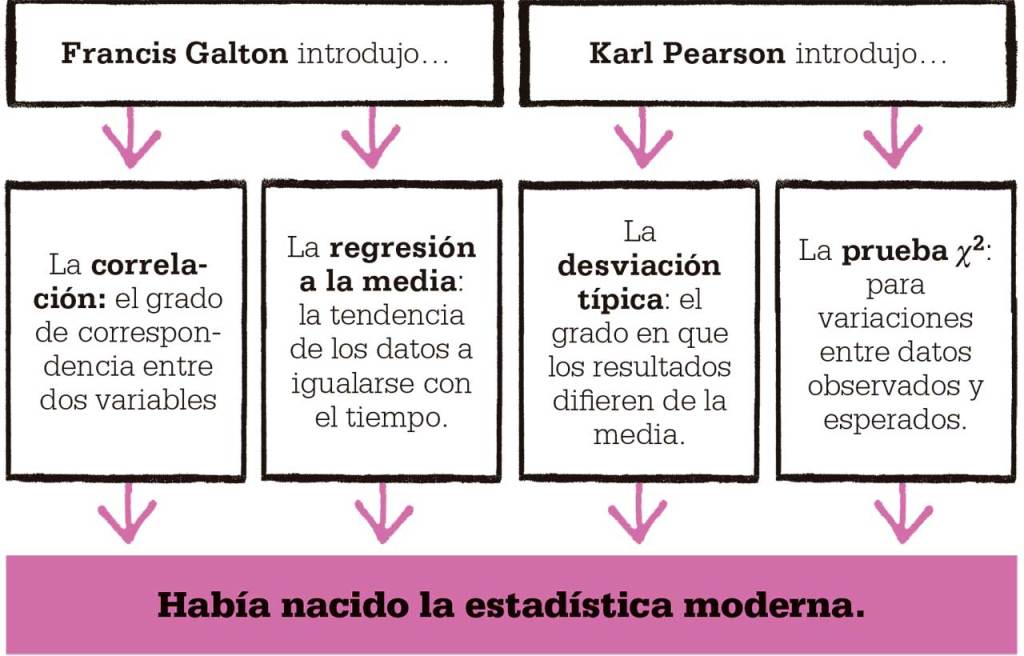
Fueron Galton y Pearson, por ese orden, quienes comenzaron a relacionar estos cabos sueltos. Galton estaba inspirado por el trabajo sobre la evolución de su primo Charles Darwin, y su objetivo era mostrar la probabilidad de que rasgos como la altura, la fisonomía y hasta la inteligencia o las tendencias criminales se transmitieran de una generación a otra. Las ideas de Galton y Pearson están ensombrecidas por la doctrina eugenésica y sus vínculos con el racismo científico, pero las técnicas que desarrollaron han encontrado otras aplicaciones. Galton era un científico riguroso, decidido a analizar los datos para mostrar matemáticamente la probabilidad de los resultados. En su innovador libro Natural inheritance, de 1889, Galton mostró cómo comparar dos conjuntos de datos para comprobar si hay alguna relación significativa entre ellos. Su aportación fueron dos conceptos hoy básicos en el análisis estadístico: la correlación y la regresión.
La correlación mide el grado en que se corresponden dos variables aleatorias, como la altura y el peso. Se suele buscar una relación lineal, es decir, reflejada en las líneas de un gráfico, en la que una variable cambia de modo acorde con la otra. La correlación no implica una relación causal entre las dos variables, sino que se limita a constatar que varían juntas. La regresión, en cambio, busca la mejor ecuación para la línea del gráfico de dos variables, de modo que los cambios de una variable se puedan predecir a partir de los de la otra.
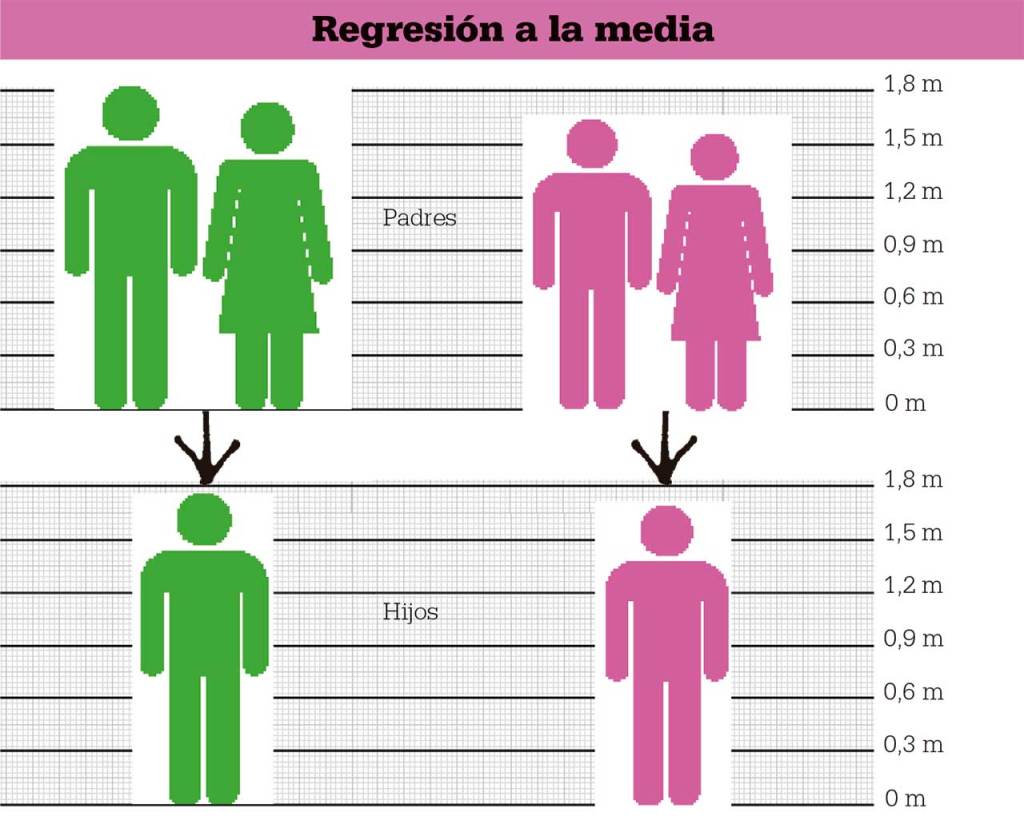
Desviación típica
El área principal de interés de Galton era la herencia en los seres humanos, pero creó una gama amplia de conjuntos de datos, destacando la medición del tamaño de las semillas producidas por plantas de los guisantes de olor, procedentes de siete conjuntos de semillas. Galton observó que las semillas menores producían una descendencia de mayor tamaño, y las semillas mayores, de menor tamaño. Había descubierto el fenómeno de la regresión a la media, la tendencia de las mediciones a igualarse, tendiendo siempre hacia la media con el tiempo.
Inspirado por el trabajo de Galton, Pearson se propuso desarrollar el marco matemático para la correlación y la regresión. Tras pruebas exhaustivas lanzando monedas y sorteando boletos de lotería, Pearson dio con la idea clave de desviación típica, o estándar, para indicar la media de cuánto difieren los valores observados de los esperados. Para obtener esta cifra, calculó primero la media, la suma de todos los valores dividida por el número de los mismos, y luego, la varianza, o media de las diferencias con respecto al valor medio, al cuadrado. Las diferencias se elevan al cuadrado para evitar problemas con los números negativos, y la desviación típica es la raíz cuadrada de la varianza. Pearson comprendió que, combinando la media y la desviación típica, podía calcular con precisión la regresión de Galton.
La prueba ji cuadrado
En 1900, tras un estudio exhaustivo de datos de apuestas de las mesas de juego de Montecarlo, Pearson describió la prueba ji cuadrado, actualmente una de las piedras angulares de la estadística. El objetivo de Pearson era determinar si la diferencia entre valores observados y esperados es significativa o un simple resultado del azar. Con sus datos sobre juego, Pearson calculó una tabla de valores de probabilidad, llamada ji cuadrado (χ²), en la que 0 indica ninguna diferencia significativa con lo esperado (hipótesis nula), mientras que otros valores indican una diferencia significativa. Pearson elaboró minuciosamente la tabla a mano, hoy estas tablas se crean con software informático. Para cada conjunto de datos se puede hallar un valor de χ², a partir de la suma de todas las diferencias entre valores observados y esperados. Los valores de χ² se cotejan con la tabla para ver la importancia de las variaciones en los datos, dentro de unos límites fijados por el estadístico, y conocidos como grados de libertad.
La combinación de la correlación y la regresión de Galton con la desviación típica y la prueba ji cuadrado de Pearson puso los cimientos de la estadística moderna. Estas ideas se han refinado y desarrollado desde ese momento, pero siguen siendo fundamentales para el análisis de datos. Esto es vital para muchos aspectos de la vida actual, desde comprender el comportamiento de la economía hasta la planificación de nuevos nexos de comunicación y la mejora de los servicios de salud públicos.
Karl Pearson
Karl Pearson nació en Londres en 1857. Ateo, librepensador y socialista, fue uno de los grandes estadísticos del siglo XX, pero fue también un defensor de la desacreditada ciencia eugenésica.
Después de licenciarse en matemáticas por la Universidad de Cambridge, Pearson se dedicó a la docencia antes de hacerse un nombre en la estadística. En 1901 fundó la revista estadística Biometrika con Francis Galton y el biólogo evolutivo Walter F.R. Weldon, seguida del primer departamento universitario de estadística en el University College de Londres, en 1911. Sus puntos de vista le llevaron a mantener frecuentes disputas. Murió en 1936.
El texto y las imágenes de esta entrada son un fragmento de: “El libro de las matemáticas”
